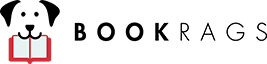+—–­+—–­+—–­+—–­+—–­+—–­+—–­+—–­+
|   |   |   |   |   |   |   |   |
| ............................. |
| . |   |   |   |   |   |   | . |
+-.-+—–­+—–­+—–­+—–­+—–­+—–­+-.-+
| . |   |   |   |   |   |   | . |
| . | ..........................|
| . |  .|   |   |   |   |   | . |
+-.-+—–.—–­+—–­+—–­+—–­+—–­+..-+
| . |   |.  |   |   |   |   . . |
| . | ................. |  .| . |
| . |  .|  .|   |   |.  | . | . |
+-.-+—–.—–.—–­+—–.—–­+.—­+-.-+
| . |   |.  |.  |  .|   .   | . |
| . | . | . | . | . |  .| . | . |
| . | ..|  .|  .|.  | . |.. | . |
+-.-+-.-.—–.—–.—–­+.—.-.-+-.-+
| . | . |.  |. .|.  .  .| . | . |
| . | . | . | . | ..| . | . | . |
| . | . |  .|. .| ..|.  | . | . |
+-.-+-.-+—–.—–..—.—–­+-.-+-.-+
| . | . |  .|.  .. .|.  | . | . |
| . | . | . | ..| . | . | . | . |
| . | . |.  | ..|. .|  .| . | . |
+-.-+-.-.—–­+.—.—–.—–.-.-+-.-+
| . | ..|   .  .|.  |.  |.. | . |
| . | . |  .| . | . | . | . | . |
| . |.. | . |.  |  .|  .| ..| . |
+-.-.-.-+.—.—–­+—–.—–.-.-.-.-+
| ..| . .  .|   |   |.  |.. |.. |
| . | ..| ............. | . | . |
|   | . |   |   |   |   |   |   |
+—–­+—–­+—–­+—–­+—–­+—–­+—–­+—–­+

]

If you will look at the lettered square you will understand that there are only ten really differently placed squares on a chessboard—­those enclosed by a dark line—­all the others are mere reversals or reflections.  For example, every A is a corner square, and every J a central square.  Consequently, as the solution shown has a turning-point at the enclosed D square, we can obtain a solution starting from and ending at any square marked D—­by just turning the board about.  Now, this scheme will give you a tour starting from any A, B, C, D, E, F, or H, while no other route that I know can be adapted to more than five different starting-points.  There is no Queen’s Tour in fourteen moves (remember a tour must be re-entrant) that may start from a G, I, or J. But we can have a non-re-entrant path over the whole board in fourteen moves, starting from any given square.  Hence the following puzzle:—­

[Illustration: 

+—–­+—–­+—–­+—–­*—–­+—–­+—–­+—–­+
| A | B | C | G " G | C | B | A |
*===*—–­+—–­+—–­*—–­+—–­+—–­+—–­+
| B " D | E | H " H | E | D | B |
+—–­*===*—–­+—–­*—–­+—–­+—–­+—–­+
| C | E " F | I " I | F | E | C |
+—–­+—–­*===*—–­*—–­+—–­+—–­+—–­+
| G | H | I " J " J | I | H | G |
+—–­+—–­+—–­*===*—–­+—–­+—–­+—–­+
| G | H | I | J | J | I | H | G |
+—–­+—–­+—–­+—–­+—–­+—–­+—–­+—–­+
| C | E | F | I | I | F | E | C |
+—–­+—–­+—–­+—–­+—–­+—–­+—–­+—–­+
| B | D | E | H | H | E | D | B |
+—–­+—–­+—–­+—–­+—–­+—–­+—–­+—–­+
| A | B | C | G | G | C | B | A |
+—–­+—–­+—–­+—–­+—–­+—–­+—–­+—–­+

]

Start from the J in the enclosed part of the lettered diagram and visit every square of the board in fourteen moves, ending wherever you like.

329.—­THE STAR PUZZLE.

[Illustration: